정렬



a = np.array([[4,3,5,7],
[1,12,11,9],
[2,15,1,14]])
anp.sort(a) # axis=-1 또는 axis=1 과 동일np.sort(a, axis=0)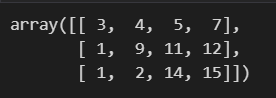
a.sort(axis=1) # a 값을 변화시킴
aargsort를 활용한 sort 방식

a = np.array([42, 38, 12, 25])
j = np.argsort(a)
j
a[j]
np.sort(a)고급 인덱싱 - 인덱스 배열을 사용한 인덱싱

a = np.array([[1,2],[3,4],[5,6]])
a
print(a[[0,1,2],[0,1,0]]) # a[0,0] a[1,1] a[2,0]을 인덱스로 하는 1차원 배열(shape=(3,))을 출력해준다.
a = np.array([[1,2],[3,4],[5,6]])
a
print(a[:,[0,1,0]])기술 통계
- 데이터의 개수
- 평균
- 분산
- 편차
- 최대/최솟값
- 중앙값
- 사분위수
데이터의 개수

x = np.array([18,5,10,23,19,-8,10,0,0,5,2,15,8,
2,5,4,15,-1,4,-7,-24,7,9,-6,23,-13])
len(x) #개수표본 평균
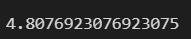
np.mean(x) #평균표본 분산

np.var(x) #분산
np.var(x, ddof=1) # 비편향 분산. 추후 공부하게 된다.표준 편차
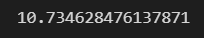
np.std(x) # 표준 편차최댓값/최솟값

np.max(x) # 최대값
np.min(x) # 최소값중앙값

np.median(x) # 중앙값사분위수

np.percentile(x,0) # 최소값
np.percentile(x,25) # 1사분위수
np.percentile(x,50) # 2사분위수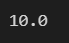
np.percentile(x,75) # 3사분위수
np.percentile(x,100) # 4사분위수난수 발생과 카운팅
시드 설정하기
- 어떤 특정한 시작 숫자를 정해주면 컴퓨터가 정해진 알고리즘에 의해 마치 난수처럼 보이는 수열을 생성합니다.
이런 기준이 되는 시작 숫자를 시드라고 합니다.
- 일단 생성된 난수는 다음번 난수 생성을 위한 시드값이 됩니다.
따라서 시드값은 한 번만 정해주면 됩니다.
np.random.seed(0) # 인수로는 0과 같거나 큰 정수를 넣어준다.
np.random.rand(5) # rand 함수는 0과 1사이의 난수를 발생시키는 함수다.
데이터의 순서 랜덤으로 바꾸기

x = np.arange(10)
x
np.random.shuffle(x) # 자체 변환 함수
x데이터 샘플링
choice 함수는 다음과 같은 인수를 가질 수 있습니다.
numpy.random.choice(a, size=None, replace=True, p=None)
- a : 배열이면 원래의 데이터, 정수이면 arrange(a) 명령으로 데이터 생성
- size : 정수. 샘플 숫자.
- replace : 불리언. True이면 한번 선택한 데이터를 다시 선택 가능.
- p : 배열. 각 데이터가 선택될 수 있는 확률.

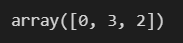

np.random.choice(5, 5, replace=False) # shuffle 명령과 같다.np.random.choice(5, 3, replace=False) # 3개만 선택np.random.choice(5,10) # 반복해서 10개 선택np.random.choice(5, 10, p=[0.1, 0, 0.3, 0.6, 0]) # 선택 확률을 다르게 해서 10개 선택
난수 생성
- rand : 0부터 1 사이의 균일 분포
- randn : 표준 정규 분포
- randint : 균일 분포의 정수 난수
rand
np.random.rand(3,5)
randn
- 기댓값이 0이고 표준편차가 1인 표준 정규 분포를 따르는 난수를 생성합니다.
np.random.randn(10)
np.random.randn(3,5)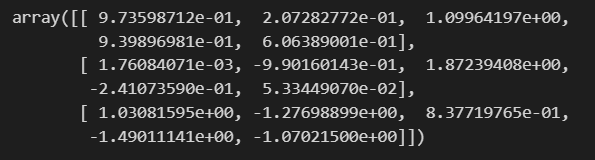
randint
- numpy.random.randint(low, high=None, size=None)
- 만약 high를 입력하지 않으면 0과 low 사이의 숫자를

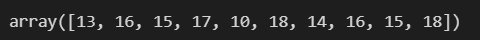
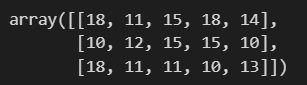
np.random.randint(10, size=10)np.random.randint(10, 20, size=10)np.random.randint(10, 20, size=(3, 5))정수 데이터 카운팅

np.unique([11,11,2,2,34,34])
a = np.array(['a', 'b', 'b', 'c', 'a'])
index, count = np.unique(a, return_counts=True)
index
count
np.bincount([1,1,2,2,2,3],minlength=6)배열의 차원과 크기 알아내기

a = np.array([1,2,3])
print(a.ndim)
print(a.shape)
c = np.array([0,1,2],[3,4,5])
print(c.ndim)
print(c.shape)
print(d.ndim)
print(d.shape)배열의 인덱싱

a = np.array([_ for _ in range(5)])
a
a = np.array([[0,1,2], [3, 4, 5]])
a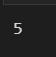
a[-1,-1] # 마지막 행의 마지막 열배열의 슬라이싱

a = np.array([[0,1,2,3], [4, 5, 6, 7]])
a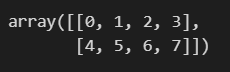
np.array([_ for _ in range(8)]).reshape(2,4)
a[0,:] # 첫번째 행 전체
a[:,1] # 두번째 열 전체
a[1,1:] # 두번째 행의 두번째 열부터 끝열까지
a[:2,:2]동전을 100번 던진 결과를 넘파이에 난수를 발생시켜서 시뮬레이션해보려 합니다.
- 앞면을 숫자 1, 뒷면을 숫자 0으로 가정하고 난수를 발생시켜 보세요.
- 이때 앞면이 나올 확률을 구하는 프로그램을 구현해 보세요.
- (seed는 0으로 합니다.)

np.random.seed(0)
coin_result = np.random.choice(2,100)
coin_result.sum()/len(coin_result)주사위는 1부터 6까지의 숫자를 가집니다.
- 이 주사위를 100번 던져서 나오는 숫자를 넘파이 난수를 발생시켜서 시뮬레이션하고 나오는 숫자의 평균을 구해보세요.
- (seed는 0으로 설정합니다.)

np.random.seed(0)
dice_result = np.random.randint(1,7, size=100)
np.mean(dice_result)